Assuming we are talking about
LaunchBar Commander..
Is there a way of create menu with favorite folders, when we click to open folder with default explorer ?
I am creating but i am getting submenu as well..
I think you are asking how to simply add items to your dock so that when you click them they open a Folder using windows explorer.
You can do so easily. Simply add an item and choose the "Command - a program, file, folder, or url" and specify the path to the
folder below where it says "Command path".
For example:
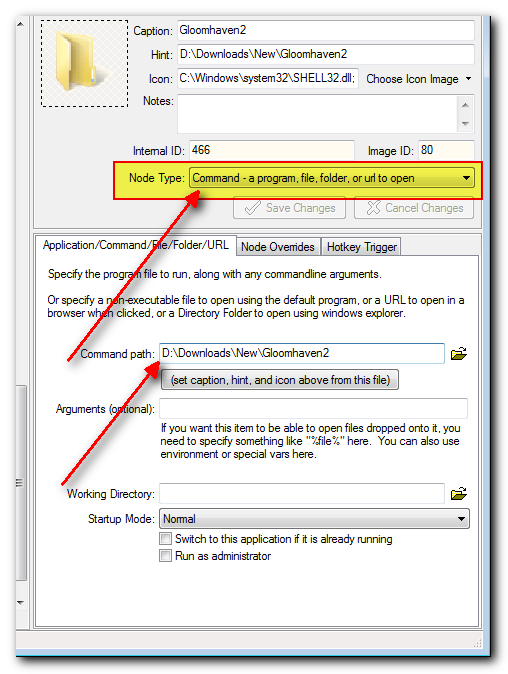
Note that you can change the icon as well to something customized.
I'll note that you can also have LBC display the CONTENTS of the menu directly if you prefer by using the "Folder" node type, but I think you probably already know that. However you may not know that if you choose this option you can still right-click on a folder and get a menu that lets you open the folder.
