Hi all,
I've been working on programming a Sudoku game and I've run into a problem with my code that I've been unable to solve for the past few days and realize I need some fresh eyes on the problem. This may not be the best place to ask about this, but as best as I can tell this problem requires a bit of an in-depth explanation and I don't really feel comfortable asking on other sites that may be more closely aligned with the specific area of inquiry, but where I have not really established myself as part of the community. And maybe it could be asked more succinctly, but unfortunately for anyone who reads this, I tend to be overly verbose in an effort to make sure I'm explaining myself clearly. So here goes.
First of all, I assume the reader is familiar with Sudoku puzzles and understands the basic rules. But I figure I should establish some Sudoku terminology (mostly
from Peter Norvig), so we're all speaking the same language here.
Square: A place where a number goes. A Sudoku puzzle is made up of 81 squares arranged in a 9x9 grid.
Row: Nine squares arranged horizontally (9x1), in which the numbers 1 through 9 can only appear once.
Column: Nine squares arranged vertically (1x9), in which the numbers 1 through 9 can only appear once.
Box: Nine squares arranged in a 3x3 grid, in which the numbers 1 through 9 can only appear once.
Unit: Any nine squares that compose a row, column, or box. Each square is a member of exactly 3 units.
Peers: Any squares that share a unit are considered peers. Each square has exactly 20 peers.
Given: The "freebie" clues that are known at the start of the puzzle.
Minimal Puzzle: A Sudoku puzzle that has the fewest amount of givens possible, while still only having one unique solution.
And here's a crude diagram showing a minimal puzzle with some of the above terminology highlighted:
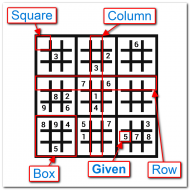 Constructing a minimal Sudoku puzzle
Constructing a minimal Sudoku puzzleSo what I'm trying to accomplish is making a game that can generate an infinite number of Sudoku puzzles (well, as many of the 6,670,903,752,021,072,936,960 possible puzzles as a player might want/be able to play). It turns out that generating solutions is easy. You can sort of just make it up as you go along. The part I'm having trouble with is going from the solution to the minimal puzzle.
In other words, in order to present the player with a puzzle to solve, I want to go from something like what's on the left to something like what's on the right:
1 2 7 | 4 5 8 | 3 6 9 . . . | . . . | . 6 .
5 3 9 | 6 7 2 | 1 8 4 . 3 . | . . 2 | . . .
6 4 8 | 9 3 1 | 7 2 5 . . . | . 3 . | . . .
------+-------+------ ------+-------+------
3 1 5 | 7 8 6 | 4 9 2 . . . | 7 . 6 | . . .
4 8 2 | 3 1 9 | 6 5 7 . 8 2 | . 1 . | . . .
9 7 6 | 2 4 5 | 8 3 1 9 . 6 | . 4 . | . . .
------+-------+------ ------+-------+------
8 9 4 | 5 6 7 | 2 1 3 8 9 4 | 5 . 7 | . . 3
2 6 3 | 1 9 4 | 5 7 8 . . . | 1 . . | 5 7 8
7 5 1 | 8 2 3 | 9 4 6 . 5 . | . . . | . . .
I've written code that accomplishes it. In fact, the above puzzle was generated by my code. But it's far too slow, and unpredictably so, to be useful in a real-time game. Sometimes it only takes a couple of seconds to generate a puzzle, which in itself is too slow. But other times it takes up to a few minutes. And in a few cases it has taken so long that I've been too impatient to let it finish. I'm coding this in GDScript, which is a custom language created for Godot, but which is very similar to Python.
I'm storing the solution of the 9x9 grid in a special kind of one-dimensional array in GDScript called a
PoolIntArray, which is passed by value instead of reference. It would look like this as a traditional array:
var answer := [
1, 2, 7, 4, 5, 8, 3, 6, 9,
5, 3, 9, 6, 7, 2, 1, 8, 4,
6, 4, 8, 9, 3, 1, 7, 2, 5,
3, 1, 5, 7, 8, 6, 4, 9, 2,
4, 8, 2, 3, 1, 9, 6, 5, 7,
9, 7, 6, 2, 4, 5, 8, 3, 1,
8, 9, 4, 5, 6, 7, 2, 1, 3,
2, 6, 3, 1, 9, 4, 5, 7, 8,
7, 5, 1, 8, 2, 3, 9, 4, 6,
]
I also have a similar array of booleans, called "givens" which indicates if a particular square is a given or not.
I then follow a method I read about in
a paper called Sudoku Puzzles Generating: from Easy to Evil (link to archive, since original link is dead) which the authors refer to as "digging holes" in the puzzle, and offer this flowchart as part of their explanation:
 Constructing a minimal Sudoku puzzle
Constructing a minimal Sudoku puzzleI'll summarize my understanding and (attempted) implementation as follows:
- Order a list of all the squares to "dig" however you see fit. (I just shuffle an array of all the squares)
- For each square in the list, attempt to dig the known value N. This means to set the value as "unknown" or "empty" (represented internally by the number 0).
- With the newly dug square, attempt to solve the puzzle with all possible values (1-9) other than N.
- If you find a solution, it means the puzzle is no longer unique (it has multiple solutions), so the square is considered a given and must display the value N to maintain uniqueness.
- If you don't find a solution, the square can remain "dug" and you continue iterating the list to dig more holes.
- Once you've iterated the entire list, you should have dug out all squares that are not essential to maintaining the uniqueness of the puzzle, which results in a minimal puzzle.
Here's the code which I think does what I described above:
# digs a solved grid to find a minimal puzzle
func find_givens() -> void:
# make a list of all 81 indices of the grid
var dig_list := []
for idx in 81:
dig_list.push_back(idx) # push_back() just adds elements to the end of an array
# randomize the order of squares we "dig"
dig_list.shuffle()
# prepare some variables we'll be using repeatedly
var nums = answer # grab a copy of the answer so we don't make changes to it
var v : int # temporarily stores the "dug" value in case we need to replace it
var coords := Vector2() # x,y coordinates
# iterate the randomized list
for i in dig_list:
# don't attempt to dig a square that is known to be a given
if given[i] == true:
# sanity check: this code should never actually be reached
continue
# store the current value of the digit
v = nums[i]
for n in range(1, 10): # iterate the numbers 1-9
# skip if this is the square's original value
if n == v:
continue
# dig the value and try finding other solutions
nums[i] = 0
# get the (x, y) coords for this square
coords = index_to_coord(i) # convert the index (0-80) to x,y coordinates as if on a 9x9 grid
# change the value at this square to something else, if possible
if is_possible(nums, coords.y, coords.x, n):
# N could legally be placed in this square
nums[i] = n
# try to find a solution to the puzzle with this new value in this square
if solve(nums) > 0:
# we found a solutions, which means the puzzle is no longer unique
# so put the value back
nums[i] = v
# mark this square as a given
given[i] = true
# don't attempt further numbers for this square
break
And here's the code for the if_possible() function, which is used to determine if a value n could legally be placed in the square located at (x,y) in a 9x9 grid. Or in other words, it makes sure that no other peer of the square (x,y) has the value n:
# returns true if no peers have the value n
func is_possible(grid, y : int, x : int, n : int) -> bool:
for i in 9:
# check if n already exists in current row (9x1)
if grid[coord_to_index(y, i)] == n:
return false
# check if n already exists in current column (1x9)
if grid[coord_to_index(i, x)] == n:
return false
# integer math here means (5 / 3) * 3 is the same as 1 * 3
var x0 : int = (x / 3) * 3
var y0 : int = (y / 3) * 3
# check if n already exists in current box (3x3)
for i in 3:
for j in 3:
if grid[coord_to_index(y0 + i, x0 + j)] == n:
return false
# as far as we know, n is a legal value for this square
return true
And finally, the code used to attempt to find a solution to the puzzle. I think this is where my trouble lies. This function basically just brute-forces the grid, attempting every possible value in every unknown square, looking for a solution, with backtracking when it reaches a dead-end. Initially I had it naively starting at element 0 of the array and looping through them in order, but this is obviously very inefficient and leads to a lot of duplicated efforts due to backtracking. It seemed to work, and generated minimal puzzles which usually had about 24-26 givens. But as mentioned previously, it was pretty slow.
So then I attempted to sort the list of squares to solve by the number of possible values that were legal to place there, starting with those which had the least possible solutions. This increases chances of success, but even in the event of a failure (dead-end) it cuts out a huge number of the possible solutions we'd have to check.
Oh, and since it's recursive, I have it keep track of and return how many solutions it has found so that it can immediately jump all the way back down the stack once a solution has been found.
func solve(grid, solutions := 0) -> int:
# this is a dictionary whose key will be the (x,y) coordinate
# and the value will be the number of possibilities for that coordinate
var possibilities = {}
# loop through every element in the grid
for i in grid.size():
# get the (x,y) coordinates for this index
var coord = index_to_coord(i)
# start with the assumption that each square has 0 possibilities (i.e., the square's value is known)
possibilities[coord] = 0
# if it's not zero, then it's considered "solved" already
if not grid[i] == 0:
continue
# check how many values are possible here
for n in range(1, 10): # iterate the numbers 1-9
if is_possible(grid, coord.y, coord.x, n):
possibilities[coord] += 1
# sorted_list is an array whose elements will contain the index of the squares grid,
# sorted by the number of possibilities
var sorted_list := []
for n in range(1, 10): # iterate the numbers 1-9
# loop through each element in possibilities
for coord in possibilities.keys(): # remember that each key is an (x,y) coordinate
if possibilities[coord] == n:
# add this square to the sorted list of squares to solve
sorted_list.push_back(coord_to_index(coord.y, coord.x))
# now iterate through the sorted list and try solving
for i in sorted_list:
var coord = index_to_coord(i)
if grid[i] == 0:
for n in range(1, 10): # iterate the numbers 1-9
if is_possible(grid, coord.y, coord.x, n):
grid[i] = n
solutions += solve(grid, solutions)
if solutions > 0:
return solutions
else:
grid[i] = 0
# none were possible, we've reached a dead end
return solutions
# if we got this far then we've solved it!
solutions += 1
return solutions
And again, this seems to work... kind of. I mean, it is (usually) noticeably faster than when I was naively brute-forcing without sorting. But (1) it's still too slow, taking at least a couple of seconds to complete, and (2) the "minimal" puzzles its generating can't actually be minimal. Doing it the naïve way, I was getting minimal puzzles with about 24-26 givens on average, the puzzles this is generating consistently have almost twice as many, usually in the 44-46 range. But it has been proven that the least amount of givens a unique puzzle could have is as low as 17 and the highest amount of givens a minimal unique puzzle can have is 39. So something is definitely wrong. Here's an example:
. . . | . 5 9 | . 3 4
2 1 . | . . 6 | . 5 7
9 . . | 3 . 7 | . 6 .
------+-------+------
. 9 . | . . 3 | 8 4 2
5 . 8 | 7 . 2 | 3 . 9
. . 2 | 1 9 . | . . .
------+-------+------
. 2 . | 8 7 1 | 4 . .
1 . 7 | 9 . . | 5 . 6
. 3 9 | 6 2 . | 7 8 .
Oh, and for completeness, here is the code for a couple of helper functions that are used in a few places in the code above:
# returns an index for an 81-element array based on x,y coordinates of a 9x9 grid
func coord_to_index(y : int, x : int) -> int:
return (y * 9) + x
# returns the x,y coordinates of a square on a 9x9 grid based on 81-element array index
func index_to_coord(i : int) -> Vector2:
var coord := Vector2()
coord.x = i % 9
# integer division
coord.y = i / 9
return coord
I tried adding tons of comments everywhere to make sure it was clear what the code was (supposed to be) doing. If anyone here takes the time to read this, parse/understand the code, and offer helpful suggestions/solutions, I'd appreciate it. Mostly I think I just needed a break from the coding and thought that maybe the process of writing this all out would be a form of Rubber Duck debugging.
I know I'm doing something wrong because I'm not getting minimal puzzles anymore. So help figuring out why that's happening would be much appreciated. But perhaps a more helpful response would explain what else I'm doing wrong that is making this so slow. My understanding is that most minimal puzzles should be solved/generated in milliseconds at most, and that it should be fairly rare to come across a puzzle that takes a few seconds and even rarer to come across one that takes minutes or longer. I've tried benchmarking my code by generating 100 puzzles and averaging the time it takes to do each step, and I can't even do that because while it "only" takes a few seconds at best for each puzzle, it often takes up to a few minutes. But the clincher is that in every attempt at generating 100 puzzles in a row there's (at least) one that takes so long that I've never had the patience to find out exactly how long it would take to complete. I can't remember for sure, but I think I've left it running on a single puzzle for over an hour before aborting the process and trying to adjust the code to speed it up.
What am I doing wrong? And where? Please don't say "everything/everywhere"

