@mouser: Was this problem ever resolved - and if so, then how?
I've "bumped" it because I have what seems to be the exact same problem. Actually, I've had the problem for quite a while now, and have only now set myself the task of fixing it - I felt sure that it was a settings/options problem, but that doesn't seem to be the case. I have been unable to make the problem go away.
The problem is: that the background in any text box that I create (whether coloured or not) remains transparent, regardless of what I do to make it opaque. The box's
border is unaffected - it is opaque. I've fiddled with the settings as per the thread above, but all to no avail.
I've been using a workaround on this for some time - I just place the text box over an area of the image being edited where the background is plain (i.e., no pattern, text or image behind it). I've been doing quite a bit of editing lately though and this workaround is becoming a PITA.
Any suggestions as to what I might be doing wrong?
(Thanks in advance.)
By the way, I am using Win10 Pro-64bit, and usually am wanting to edit images stored in the CHS database. SC works just fine otherwise.
Here are 2 screenshots of what it's doing.
For the first screenshot, I've put the shadow on the box border to demonstrate that is working OK.
Setting the box transparency to 0 or 255 seems to make no difference, but whilst I am editing the text box it becomes temporarily opaque-white - as per the 2nd screenshot (note the shadow has disappeared whilst I am doing that).
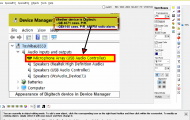 Text box background problem
Text box background problem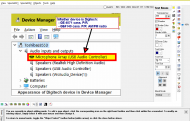 Text box background problem
Text box background problem
