Introduction
Welcome to WCP, the FIFA World Cup Markov Chain Monte Carlo Tournament Predictor and Bet Advisor. It was originally implemented for the 2006 Fifa World Cup and then updated for the 2010 FIFA World Cup.
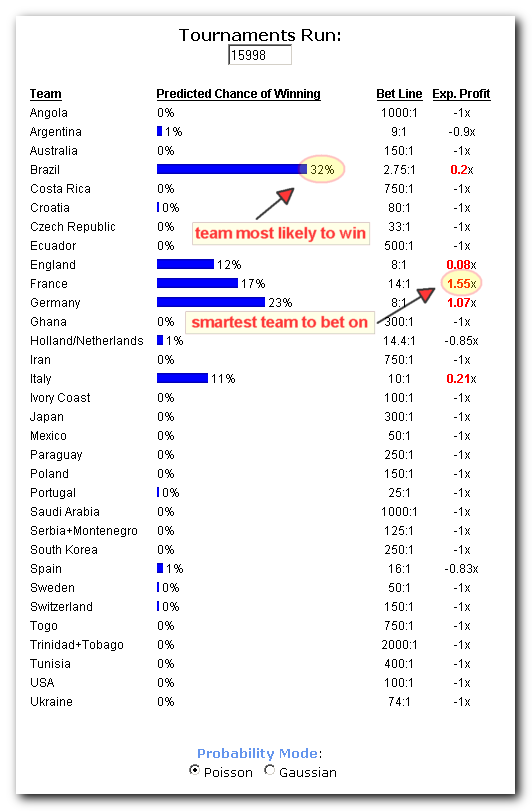
This online tool predicts the odds of teams winning and, more importantly, helps you identify the smartest bets to make with the best expected payoffs, which usually do not involve betting on the team most likely to win.
Support the Authors
Other Resources
Winingware License
What is winningware? It's just a term we made up - it means that if you win some money you should send us a thank you and donate a little of your winnings to us. And if you lose money, promise not to blame us.
Occasionally a friend of DC without a web site will release a program and ask us to host it. We've create the Miscelaneous Member Software Archive for this purpose.
There you will find some programs by DC member seedling, including: Random MixTape Maker, which takes a large collection of your mp3 files and creates playlists with a specified target duration; WTF Music Info, which will scan your music directories and give you a nice, graphical view of your music library.
- Number of programs available: 3
- Last updated: 2008
- Visit the miscelaneous DC member archive page to browse apps and download them here: http://www.dcmembers.com/archive.
The World Cup Predictor (Markov-Chain Monte Carlo) and Bet Advisor
This online tool (WCP) performs two main functions. Firstly, it uses Markov Chain Monte Carlo techniques to estimate the likelyhoods of each team winning the FIFA World Cup tournament -- using the pairwise probabilities for each team matchup provided by users. Secondly, it uses these estimates, and the current betting odds found online, to identify the bets with the highest expected values.

What Is Markov Chain Monte Carlo?
Markov Chain Monte Carlo (MCMC) algorithms work by repeatedly simulating a sequence of progressive events over and over, and accumulating statistics on final outcomes.
MCMC works by leveraging simple single-event probabilities, that you can easily estimate, into long-range predictions involving many interactions. There's no magic involved. It's basically a way of estimating the probabilities of complex multi-step outcomes by average many outcomes of brute force simulation.
MCMC and the World Cup
In the case of the World Cup, MCMC amounts to simulating complete tournaments by playing each game from round one through the final, choosing winners based on simple pairwise expectations of how the teams pair up against each other.
The pairwise match-up probabilities are the key to being able to simulate entire tournaments autonomously, and must be provided by an expert or from records of previously played games. You can create your own pairwise estimations using WCP'10 or use one of the probability estimation tables generated by an expert.
Obviously, the accuracy of this pairwise match-up table is critical to getting good results from the Tournament Simulator. The key to the power of MCMC methods is that they let you convert simple known (or relatively easily estimable) probabilities, and by simulating full sequences of outcomes over and over again, arrive at an estimate of the probabilities of different long-term highly-interactive final outcomes.
There are some important caveats to keep in mind. The MCMC approach has the potential to give an extremely accurate estimate of the probabilities of each team winning the tournament, assuming that one can come up with an accurate model of the distribution of game scores likely to result when a given pair of teams meet up. However, this assumption is a generous one, and that is where the trouble starts.
A Perfect Probability Function?
There is no objectively perfect model of the probability distributions of game scores between any two teams, and there are tons of choices for functions to represent probability distributions. This is where we must choose some approximate parameterized function to represent the range of probability distributions of possible game scores. Our goal is a probability distribution function that can capture a reasonable range of match-ups, and which is reasonably easy for an expert to express.
For psychological reasons involving motivation - in a real match game there may be some more complex interaction between team scores in a match, but this seems unlikely to have a significant effect on which team wins the game.
Truncated Gaussian and Poisson Distributions
To represent the probability distribution of scores in a game, we use either a Truncated Gaussian or a Poisson distribution, with user specified means (and standard deviations in the case of a Gaussian). For each possible game match-up (i.e. every pair of teams), an expert must provide an estimate of the mean number of goals scored by each team. The mean values can be seen as a kind of average score if the two teams played over and over again.
If using Truncated Gaussian functions for the distribution of scores, an expert also needs to provide an estimate of the Standard Deviation of the provided means. The standard deviation can be seen as a measure of the noise in the estimate. More precisely, it is a measure of the average distance of the data values from their mean. The larger the standard deviation, the more randomness that will result when the games are simulated. With standard deviations of 0, the expert is saying that he is 100% confident of the exact score of the game. Larger values reflect less confidence (or more innate randomness). Random numbers generated from the Gaussian are rounded and truncated at 0. Standard deviation parameters are ignored when using Poisson distribution.
Which probability Function Should You Use?
You can choose which probability distribution to use. In practice we don't expect much difference between using a Gaussian and Poisson distribution. The Poisson is a bit simpler since it does not require a Standard Deviation value to be provided. You might use a Gaussian if you want to experiment with standard deviations other than 1.0. Larger values induce more noise; smaller values put the simulated game scores close to their means.
Round One - Groups and Rankings
Why not just estimate the probability that each team will beat each other team? Good question. You could make a good case that such an estimate would be easier for experts to provide, rather than score distributions. The problem is the way the first round of the FIFA World Cup tournament is conducted. It's not a simple elimination process, and is instead based on points scored.
To use simulated games to predict a tournament winner we need to actually simulate the entire tournament according to FIFA rules. The official tournament rules are a bit unusual and complicated.
The first round is a "knock-out" round, where teams are organized into 8 groups of 4 teams. Within each group, 6 games are played, so that each team plays each of the others in their group. Then the top 2 "ranked" teams in each group advances to the second round.
We must simulate this ranking process. For each game played, a team gets +3 points if they win, and +1 point if they tie. If the top two teams in a group cannot be uniquely chosen based on points, they are ranked based on highest goal differential, and then total goals. If this is still not enough to determine the top two ranked teams uniquely, they are compared based on performance playing each other. If this fails, FIFA judges do something crazy to pick a winner. We simulate all of these ranking procedures except the last two. While we could use head-to-head performance to break ties in that penultimate case, we decided it was so rare as to be not worth the effort. If it gets this far we simply choose randomly between teams tied for ranking in the top two positions.
Elimination Games and Free Kicks
After the first round, things get much simpler and FIFA employs a standard elimination tournament where after each game the losing team is eliminated from the tournament. The only slightly tricky issue is how to force a winner when the simulated scores show a tie initially. In the actual game, a series of free kicks will determine a unique winner. In an ideal world one might try to use separate probability distributions to model free kick performance of the different teams, but our strong intuition is that such modeling is overkill. Instead, we simply simulate the breaking of predicted ties by running additional simulated games between the teams. This amounts to assuming that the likelihood of a team winning in free kicks against their opponent is matched by their likelihood of winning against their opponent in normal scoring.
Going One Step Further -- Identifying the "Sweet" Bet
When deciding what to bet on, you don't care as much about actual chance of winning as you do about your expected profits in the long run: